Elvenar Event Chest Strategy Analysis

EDIT: The calculators are up to date with all the chest events up to and including Rise of the Phoenix Cult (March 2021).
Another major Elvenar event – Summer Solstice – is rapidly approaching, and it is time to do some analysis of what chest opening strategy we should employ, and what rewards can we get as outcomes of that. But instead of doing analysis on some specific strategies only, we’ve created a couple of calculators that can answer many of those questions for any particular strategy or targeted rewards!

Intro (also TL;DR)

Every now and then, there is a major event running in Elvenar. Every now and then is about 4-5 times a year, and major means that it runs for about 3-4 weeks. You can take a look at Main Event Overview in the Elvenar Wiki. You earn event currency (e.g. Sky Essence, Sun Flares etc) by completing event quests, and then you can spend this event currency opening different chests that give out variety of randomized rewards – grand prize tokens (e.g. Feathers, Flowers etc), daily event prizes, instants, KPs etc. As every Elvenar event chest rewards are different, we always wonder what is the best strategy for opening the chests? I.e. which chests should we open? And related question is, how much of each reward can we expect to get from a particular event? Well, we’ve got some nifty calculators for you that would help to answer those questions!

Calculators!

The rest of the post describes some of the ways you can use those calculators. But really, if you played any of the previous events and are familiar with the mechanics, this should be rather straightforward. So you can jump right into it! Here they are:

• Manual Event Chest Strategy calculator
  • Here you define your own Elvenar event chest-opening strategy manually (i.e. you specify priorities for chests), and this calculator can tell you what are the expected outcomes of this strategy for all the rewards.
• Optimal Event Chest Strategy calculator
  • But why would you want to figure out a strategy by yourself? Ultimately, you just want to focus on particular rewards, and this calculator can figure out an appropriate Elvenar event chest-opening strategy specific for the rewards you are targeting. And yes, you can target more than one reward!

We’re describing these calculators in more details below, so keep reading if you want more information. Keep in mind that your individual results might be quite different from the expectations outlined in this analysis. That’s probability and statistics for you 😉

Setup

Chests

Let’s quickly reiterate the setup. We will be using Evolution of the Phoenix event as an example, but the calculators support multiple events, and hopefully can be easily extended in the future as long as overall mechanics is the same or similar.

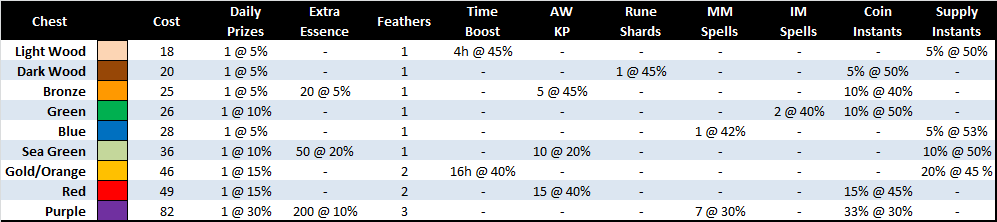
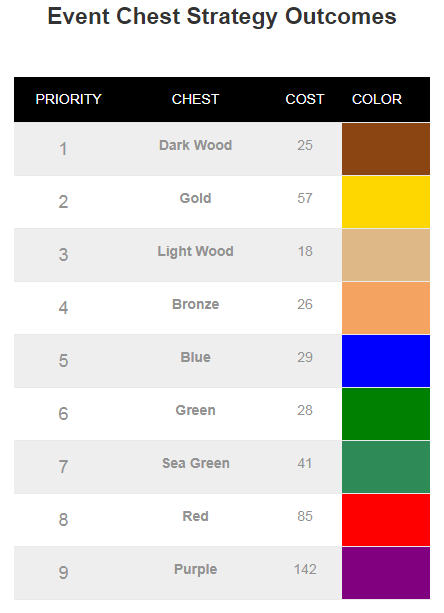
So, there are 9 different chests out there, that need different amounts of event currency (e.g. Sky Essence) to open. Here is a summary for the EotP event:

There are always 3 chests available at any time. Once you open one of them, another 3 will be drawn at random (presumably). And every time you open a chest, you get guaranteed number of grand prize tokens (Feathers), and one of the chest prizes at random (see the table above). This sometimes includes a chance for extra event currency.

Grand Prizes

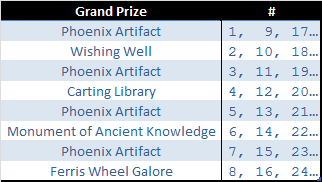
Once you accumulate 20 grand prize tokens, you get the next Grand Prize in the sequence. The sequence for EotP event looks like this:

It is looping, so once you reach the last grand prize on the list, you start with the first one again. One caveat though – only first 20 grand prizes cost 20 grand prize tokens. Starting from GP #21, you need 30 tokens to get the next grand prize. Generally, it is only relevant for players who paid for extra essence one way or another, as with maximum amount of event currency available for free it is practically impossible to reach 30 tokens tier. Here is a caveat for using the calculators – they currently do not take into account cost increase for the grand prizes. This is generally immaterial for free players, but if you’re planning to buy a lot of extra event currency (one way of another), then grand prize results will be overstated.

Event Currency

You get event currency (e.g. Sky Essence) by completing main line quests (can be done one right after another), daily quests (one quest a day only), as well as picking 1-3 event currency items dropped randomly around the city (hourly intervals, up to 6 drops at the same time max).

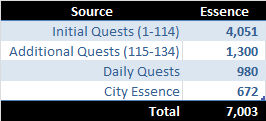
So how much event currency you can get for free? Well, here is an optimistic calculation for the EotP event:

As long as you complete all the quests, the event currency from quests is guaranteed. City event currency assumes that you pick up 24 drops a day from the city. This is difficult to do as there are only 24 drops a day, with mostly 1 event currency each. But it is not impossible.

Each event is different, as well as each player can have different levels of participation. So you will need to input total event currency that you expect to get from the source above. For instance, for the EotP event max free player can use 7,000 of total event currency. Note, that this does not include event currency from the chests as this will be taken care of as part of the calculation (so the actual event currency spent will likely be higher than what you did input).

Strategies

Alright, so now that the general mechanics is clear, we can talk about the chest-opening strategies. When we talk about strategy for opening Elvenar event chests, all we really mean is a priority sequence for the chests. You get your 3 chest selection, and then you always pick the one that has the highest score as per your strategy.

Manual Event Chest Strategy setup

First, let’s look at the Manual Event Chest Strategy calculator. Its input consists of two main parts: event definition and manual strategy definition.

Event Definition

So this is how event definition section looks like:

This is rather self-explanatory. The only thing is, you will need to figure out how much of the event currency you are planning to get for a particular event (see Event Currency section above).

Manual Strategy Definition

Strategy definition section looks like this:

In this section you need to assign priority to each chest. Priority can be any number – the important part is which chest has higher or lower number attached to it. Lower numbers mean higher priority.

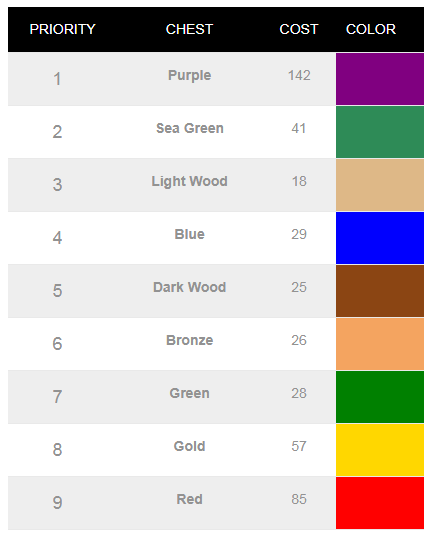
This defines your Elvenar event chest-opening strategy – the next time you have a draw of 3 chests in the event, you will be picking the chest with the highest priority out of the three. In the example above, you will pick Light Wood chest every time it shows up in the draw. You will pick Dark Wood chest every time it is in the draw and there is no Light Wood chest there etc. This also means that you will never pick Red and Purple chests, as there will always be a higher priority chest in the 3 chest draw.

And now, after you press the “Calculate” button, you will find out what can you expect from this particular customized strategy for opening event chests in Elvenar. 

Optimal Event Chest Strategy setup

Now, let’s look at the Optimal Event Chest Strategy calculator. Its input also consists of two main parts: event definition and value target definition.

Event Definition

Event definition is exactly the same as for Manual Event Chest Strategy calculator:

Again, the only thing you will need to figure out here is how much of the event currency you are planning to get for a particular event (see Event Currency section above).

Value Target Definition

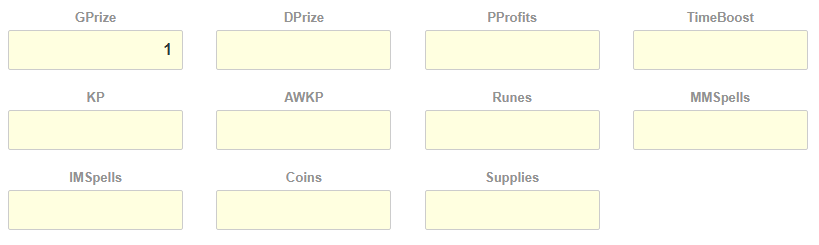
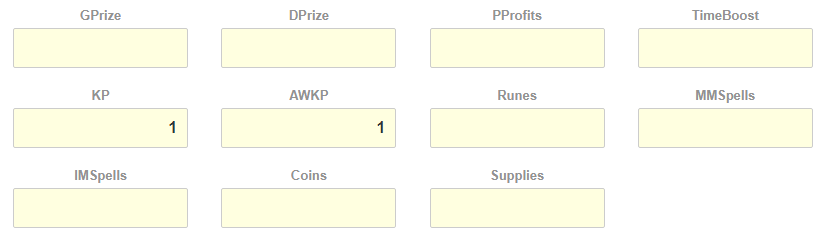
Value target section requires a bit more explanation. It looks like this:

Here, you basically define what is it that you’re going for in the event, or how much you value each reward relative to each other.

Short-hands should be relatively obvious, but measurements are not necessarily so. So here it goes:

• GPrize – Grand Prizes, number of units
• DPrize – Daily Prizes, number of units
• PProfits – Portal Profit Instants, in %
• TimeBoost – Time Boosters, in hours
• KP – Knowledge Points, number of KPs
• AWKP – KP instants (to be deployed into Ancient Wonders), number of KPs
• Runes – Rune Shards, number of units
• MMSpells – Magical Manufactoring spells, number of units
• IMSpells – Inspiring Meditation spells, number of units
• Coins – Coin Rain instants, in %
• Supplies – Supply Windfall instants, in %

It’s easier to explain value targeting with examples, so let’s look at how it works.

Maximize Single Reward

So let’s say you only care about a single reward type, and want to maximize that regardless of how much you’re going to get in terms of other rewards. This is a fairly straightforward setup. You put 1 of the reward you’re interested in, and 0 (or blanks) for all other types. For instance, if you want to maximize your Grand Prizes regardless of everything else, then you put 1 into GPrize box, and zero or blanks everywhere else. This is setup in the screen above.

Maximize Multiple Rewards

Now, if you want to balance focus on more than one prize type, you need to enter less trivial value targets. Lets say that you’re equally interested in Grand Prizes and Daily Prizes. Then you enter 1 for GPrize and 1 for DPrize, and everything else is 0. If you value 1 Grand Prize as 2 Daily Prizes then you enter 2 for GPrize and 1 for DPrize, to measure in DP units. Alternatively, you can enter 1 for GPrize and 0.5 for DPrize to measure in GP units. This doesn’t change the strategy or actual outcome, only display for Total Value.

Remember the units of measurement though. E.g. TimeBoosts are measured in hours, PP, Coins and Supply instants are measured in %, so if you want to focus on daily prizes, portal profits and timeboosters, and you value them in 100:4:5 ratio, then you enter 1, 0.04 and 0.05 in corresponding weights (to measure in DP units). This is equivalent to saying that you value 1 DP, 25% worth of PP and 20 hours worth of time boosters equally.

Don’t overdo it! 😉

You can in theory enter corresponding weights for all the reward types. You probably don’t want to do that. Unless you can nail equal values for all disparate reward types (do you really have a solid view on how many hours of time boosters are equivalent to 1 IM spell?), your results will be suboptimal. Just focus on 1-3 value targets that you really care about, and ignore the rest.

And remember, the value section is entirely subjective! There is no fundamental view on how much different rewards relate to each other. Different players may have very different setups, and will need to deploy different strategies to achieve their maximum value!

Event Chest Strategy Outcomes

Both calculators display outcomes in the same format. Again, we have two parts – one is the strategy definition, and another one is expected outcomes. Lets take a look at both.

Strategy Definition

Strategy definition section in the outcomes looks like this:

Now, for the manual chest event strategy calculator this table simply re-formats the definition that you already provided on the setup page. Only here it is reordered in priority sequence, and has some extra data to allow for easier selection of the right chest (cost and color).

For the optimal chest event strategy calculator though, this is a calculated Elvenar event chest strategy that maximizes the total target value. And the target value (for single or multiple rewards) is what you defined on the setup page.

Expected Outcomes

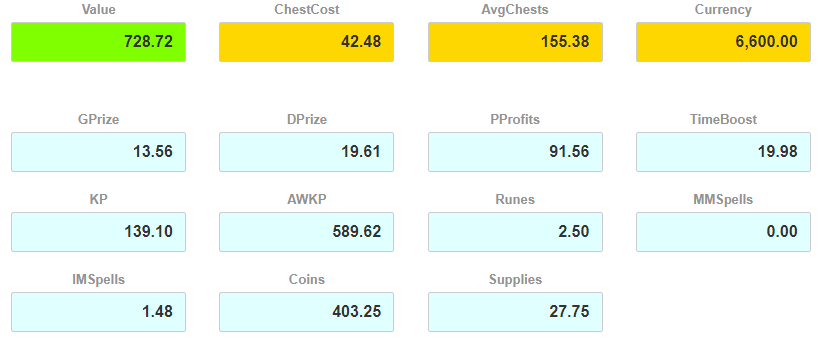
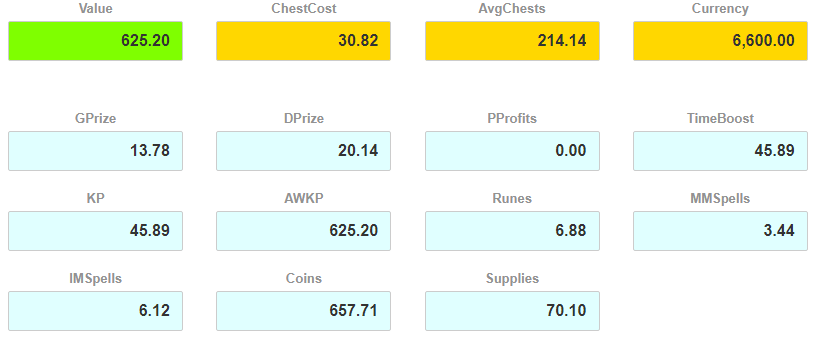
And here is a section that we’ve all been waiting for – expected outcomes of chest opening strategies. Here is how it looks like:

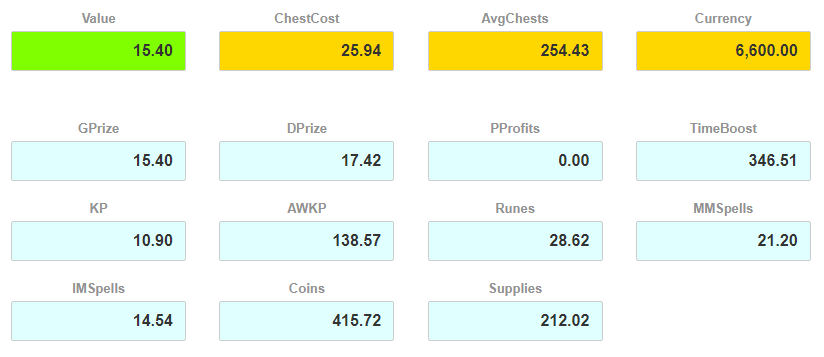
Value field is populated with the maximized target value. It is blank for the manual event chest strategy calculator as there is no optimization involved. In this screen above we were maximizing for a single reward, namely Grand Prizes. Unsurprisingly, our Value is the same as GPrize. This would always be the case for optimizing for a single reward.

Currency is the Total Event Currency that you entered on the input screen. ChestCost is the average cost of a chest while running a particular strategy (adjusted for potential event currency rewards). And AvgChests is how many chests you expect to open while running this strategy over the whole Currency amount.

So for a sample strategy that we did analyze here with 6,600 of event currency to play with, here is what we can expect:

• ~15.4 Grand Prizes. This is the maximum possible expected value given the total event currency amount as that’s what we optimized for.
• ~17.4 Daily Prizes.
• We expect no Portal Profits whatsoever.
• 346 hours worth of time boosts.
• 11 KPs, but more than 138 AW KP instants.
• 29 rune shards
• 21 MM spells and slightly less than 15 IM spells
• 415% worth of coin instants and 212% worth of supplies instants.
• We will expect to open ~254 chests.

Multiple Rewards Targeting Example

Lets look at a few more examples of how targeting multiple rewards works, and how it can be different from targeting single rewards.

Leveling Ancient Wonders

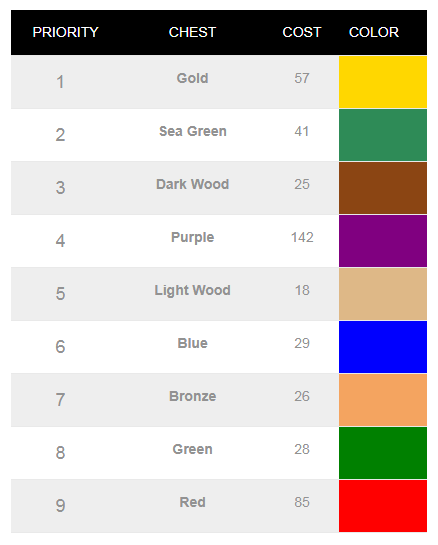
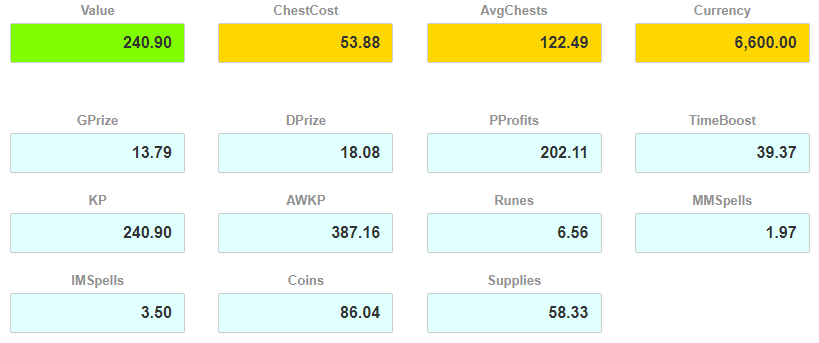
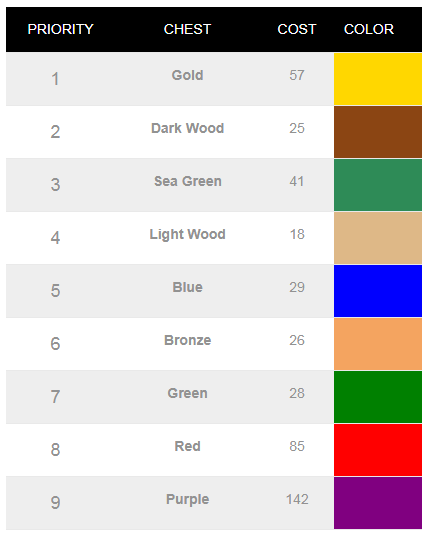
So lets imagine that you want to focus on leveling your AWs. Say you don’t care about most of the other rewards in the event. This means you’re interested in KPs and AW KP instants – and you’re indifferent as to which one you will get as both can be contributed to AWs. So in this case, 1KP = 1 AW KP. This is how we will setup our optimal event chest strategy calculator (this is for Summer Solstice event and 6,600 Total Event Currency):

Here is how the optimal strategy looks like:

And here are the expected outcomes:

This tells us that we expect to get about 139 regular KPs, but also slightly less than 590 KPs in AW KP instants. The total that we can contribute to AW leveling is 139+590=729 KPs. Which is what we see in the Value field as we assigned targeted value weights of 1 to both (1 KP = 1 AW KP).

Focus on KPs

So lets see how is it different from focusing on single reward – in this case, regular KPs. To set this up we specify 1 in the KP box for targeted value, and zero or blanks everywhere else. This is the strategy which is optimal for that:

As you can see, the strategy itself is different than the one where we optimized for both KPs and AW KPs. So what about the outcomes? Here they are:

So with this strategy, we expect to get about 241 regular KPs and 387 AW KPs. So we clearly did better on the regular KPs part – 241 is much better than 139. This is not surprising – this strategy is supposed to produce the maximum KPs. But what about total KPs available for our AW leveling? It is 241+387 = 628 KPs. This is quite a bit less than 729 KPs for the previous strategy when we targeted both!

Focus on AW KPs

So what would happen if we focus on AW KPs as a single reward instead? To set this up we specify 1 in the AW KP box for targeted value. We put zero or blanks everywhere else. This is the strategy which is optimal for that:

As you can see, the strategy is again different from either of the two strategies above. So what about the outcomes? Here they are:

So with this strategy, we expect to get only about 46 regular KPs, but about 625 AW KPs. So again, we clearly did better on the AW KPs part this time – 625 is better than 590. Again, this is not surprising – this strategy is supposed to produce the maximum of AW KPs. But what about total KPs available for our AW leveling? It is 49+625 = 674 KPs. This is still not quite as good than 729 KPs for the strategy when we targeted both!

Keep in mind that absolute value of Value field cannot be compared when targeted values are different. E.g. in this example Value is 625 as we only maximize AW KPs. We can’t directly compare this with Value of 729 that we’ve got from the combined target as 729 accounts for both KP and AW KPs. With the strategy above we still get some KPs, but we don’t take these into account when optimizing, hence Value field doesn’t include it.

Conclusion

So here you have it. I hope this analysis would be useful in order to plan your approach to any of the major events in Elvenar. More importantly, it might be useful in order to adjust your expectations 😉 And as we all may have differences in how much value we see in different rewards, you can tailor your Elvenar event chest opening strategy to what’s valuable for you. So good luck with the events, and I wish you to stay on the right side of randomness! 😉